Voici une page généraliste qui a pour but d'expliquer le principe des commutateurs et de montrer comment l'exploiter pour la résolution de nombreux casse-têtes.

1 - Qu'est-ce qu'un commutateur ?

La notion de commutateur est tout d'abord une notion mathématique de théorie des groupes. Dans un groupe, on appelle commutateur un élément noté [a,b]=aba'b' où a et b sont deux éléments du groupe et a' et b' leur inverse. a et b commutent si et seulement si [a,b] est l'élément neutre du groupe.

Cependant, ce n'est pas tant leurs propriétés mathématiques que leurs effets sur les casse-têtes qui nous intéressent. Avant d'aller plus loin, je tiens à remarquer que tous les commutateurs ne sont pas intéressants pour la résolution de puzzles de type Rubik's cube, ou du moins, pour être plus juste, tous n'ont pas le même intérêt.

En effet, prenons le commutateur [R,U] = RUR'U' sur un 3x3x3. Il réalise un cycle de trois arêtes (un 3-cycle, donc) et une double transposition de coins. Le défaut de cette formule est qu'elle déplace un peu trop de pièces. Son utilisation est donc difficile (quoique pas impossible) pour résoudre un 3x3x3.

On comprend dès lors qu'on préférera les commutateurs ne faisant bouger qu'un minimum de pièces. Pour des raisons mathématiques, il est souvent obligatoire de déplacer un minimum de trois pièces (comme sur un 3x3x3 où il est impossible de n'échanger que deux arêtes ou deux coins). On essayera donc au maximum de trouver des commutateurs réalisant un 3-cycle.

2 - Principe de construction d'un "bon" commutateur :

Un bon commutateur doit donc déplacer le minimum de pièces.

Pour réaliser cette opération, on procède ainsi :
- On réalise une suite de mouvements qu'on note A dont l'objectif est de remplacer une pièce (1) par une autre (2).
- On échange (2) avec une autre pièce (3) par une suite de mouvements qu'on note B.
- On exécute A' puis B' ce qui a pour but d'envoyer (1) à la place de (3), tout en remettant les autres pièces du casse-tête à leur place.

Au final, (1) est remplacé par (2), qui est remplacé par (3), qui est remplacé par (1). On a réalisé le cycle 1 -> 3 -> 2 -> 1. On le note (1 3 2) en mathématiques.

Pour que cette méthode fonctionne bien, il est nécessaire que les suites de mouvements A et B n'interfèrent pas trop entre elles (Je pourrais être plus précis mais je n'ai pas envie de compliquer un peu plus le propos).

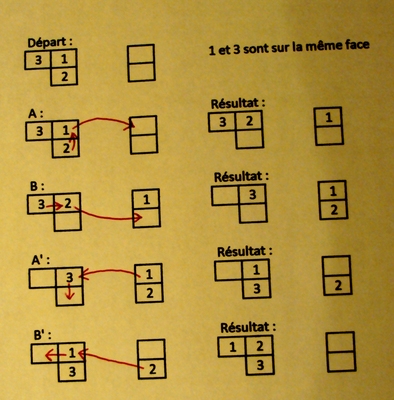
Dans le meilleur des cas, on fera en sorte que A ne remplace qu'une seule et unique pièce (1) d'une face (appelée pivot dans la suite) par une pièce (2) située ailleurs, de façon à ce que B, par une simple rotation de cette face, remplace la pièce fraîchement arrivée (2) par une autre (3) de cette même face. A' renverra donc (3) à la place initiale de (2) et la remplace par (1). Enfin, B' envoie (1) à l'emplacement initial de (3) et ramène (2) à la place initiale de (1).

 

J'ai repris les notations de la partie précédente. 1, 2 et 3 sont les pièces à déplacer et les deux T les emplacements de transit. Les deux premières photos représentent la position de départ. On a trois pièces à faire cycler. 3 doit aller à la place de 2, 2 à la place de 1 et 1 à la place de 3. 

On note L et R les "faces" du Dino qui vont intervenir dans le commutateur intéressant.

On utilise le commutateur [R',L] = R'LRL'. Dans cet exemple, on a donc A = R' et B = L. La face L, entourée de lignes vertes, est celle qui constitue le pivot du commutateur : c'est sur cette face que se situent les deux pièces 1 et 3. Et c'est sur cette face que le mouvement A remplace une pièce sans rien modifier d'autre. Ainsi, on peut faire tourner la face (mouvement B), de sorte à remplacer la pièce nouvellement arrivée par une autre de la même face. En refaisant A puis B à l'envers, on remet le cube dans son état initial.

Les quatre photos qui suivent montrent le résultat de chaque étape du commutateur. On retrouve exactement le déroulement indiqué dans la partie 2.
 

 

Ici, A = R'D'R et B = U'. Le commutateur est [A,B] = R'D'RU'R'DRU. Les images 2 à 5 donnent le résultat de chaque étape A, B, A' et B'. Le pivot est la face U.

Cet exemple permet, je trouve, de bien comprendre ce que doit être un bon commutateur. Le mouvement A a pour effet de remplacer le coin 1 par le coin 2. Mais remarquons bien que pour la face U, c'est la seule pièce modifiée par A. Ainsi, B ne fait que remplacer le coin modifié par le coin 3. A' reconstitue le cube sans rien altérer, ce qui est normal puisqu'à part la face U qui a tourné, rien ne s'est produit entre la fin de A et le début de A' : le reste du cube n'a pas été modifié et A' remet forcément à leur place toutes les pièces qui ont été déplacées par A. On retrouvera exactement la même logique sur la Dayan Gem III.

Bien des algorithmes sont inspirés de ce principe. Le classique Niklas du 3x3x3 (RU'L'UR'U'LU = [R,U'L'U] Le pivot est la face B) est une variante de ce principe.

 
Précisons un peu les notations. U est la face du dessus, F la face de devant supérieure et f la face de devant inférieure. 1, 2 et 3 sont trois coins de la Dayan Gem III.

Ici, A = F'fF et B = U. Le commutateur est [A,B] = F'fFUF'f'FU'. Les images 2 à 5 donnent le résultat de chaque étape A, B, A' et B'. Le pivot est la face U.

On exploite sur cet exemple le même principe que dans l'exemple précédent : le mouvement A ne modifie qu'un seul coin de la face U, ce qui permet de tourner cette dernière librement afin de remplacer le coin modifié par le coin 3. Je ne détaille pas la suite, j'espère que vous commencez à comprendre !

J'ai pris comme un exemple un 5x5x5. On veut ici, en apparence, échanger les deux centres mal placés. Je dis bien en apparence car, comme très souvent, il n'est pas possible d'effectuer une simple transposition. On va donc réaliser un 3-cycle et pour cela utiliser un commutateur.
 

Ici, A = dr'd'r (qui, remarquez, est déjà un commutateur !) et B = U. Le commutateur est [A,B] = dr'd'rUr'drd'U'. Le pivot est la face U.

La cinquième image montre l'état du cube après A. Le résultat de cette étape est que 2 se trouve alors à la place de 1.

L'image d'après, B = U envoie 3 à la place de 2. A' redescend 3 à la place initiale de 1 et B' replace 1 et 2 là où ils doivent être.

Une fois qu'on a compris ce qui se passe dans cet exemple, on peut généraliser ce procédé à n'importe quel cube et n'importe quel emplacement.

f) Les centres du Face Turning Ocathedron :
 

On utilise ici A = R'LR et B = M'. Le commutateur est [A,B] = R'LRM'R'L'RM. Le pivot du commutateur est la tranche M. Encore une fois, le mouvement A ne modifie qu'une seule pièce sur le pivot : seul le centre 1 est remplacé par un autre (2) sur la tranche M. On peut alors exécuter le mouvement B (M' mais on pourrait aussi faire M) qui n'a pas d'incidence sur le reste du casse-tête.

C'est toujours le même principe !

Le principe est relativement simple. Imaginons que nous sachions faire cycler trois pièces d'un casse-tête à l'aide d'un commutateur noté B à la condition qu'elles se trouvent exactement à trois positions données 1, 2 et 3. Imaginons que nous devions faire cycler trois pièces non forcément situées aux emplacements 1, 2 et 3. On commence alors par réaliser une série de mouvements notée A qui ramène chacune des pièces à faire cycler sur les emplacements 1, 2 et 3. On exécute alors B qui fait cycler les trois pièces qui nous intéressent. B ne déplaçant rien d'autre que ces trois pièces, on peut ensuite exécuter A' pour tout remettre en ordre et renvoyer les pièces à présent déplacées aux trois emplacements qu'elles occupaient avant la manipulation.