Voici une solution simple, bien que très longue, permettant de venir à bout de la Brain Ball.

Tout d'abord, posons quelques notations :
 

La rotation autour de l'axe principal (trait vert) sera notée T (La partie où il est écrit "BrainBall" ne tourne pas). Un nombre  X désigne la rotation de la roue numérotée dans le sens horaire de X treizième(s) de tour. X' désigne le même mouvement mais dans le sens anti-horaire.

La formule magique est : T6T6'T1T6'T6T1', qui n'est pas tout à fait un commutateur, mais qui permet de réaliser deux transpositions simultanées (celles des nombres 3-4 et 7-8 de la photo).

La méthode se décompose en deux étapes :

1) Faire en sorte que toutes les pièces aient la même orientation.

Attention ! Il n'y a qu'un sens possible. Par exemple, sur ma Brain Ball, le côté blanc des pièces doit se trouver du côté où il y a l'inscription "BrainBall". Si on se trompe de sens, on tombe sur un problème de parité insoluble (on ne peut pas finir la résolution car il reste obligatoirement deux pièces à échanger à la fin, ce qui n'est pas possible).

Pour réussir cette étape, il faut faire fonctionner son intuition, et éventuellement finir en utilisant l'algorithme suivant : T2T2'T. Il retourne la pièce 7 de la photo (en déplaçant pas mal de chose, cependant) sans retourner d'autres pièces.

Pour tout retourner, utiliser T5T5T (Attention, là encore on déplace pas mal de pièces !).

2) Remettre les nombres à leur place.

On utilise pour cela l'algorithme donné ci-dessus, éventuellement combiné trois fois de cette façon :
(T6T6'T1T6'T6T4)x2 T6T6'T1T6'T6T4. Cette longue formule permet le cycle des pièces 2 -> 3 -> 4 -> 2 de la photo.

Autant dire que c'est long ! Je n'ai pour l'instant pas trouvé mieux. J'éditerai cette page si je trouve un jour comment faire plus rapide !

EDIT : Bon, pour faire le même cycle exactement, on peut faire beaucoup plus court : T6T6T6T6'T1T. Bien plus efficace pour exactement le même résultat !

Tout d'abord, posons une notation :
 

 

On notera L4 le fait de tourner la roue gauche de 4 billes dans le sens horaire, R-3 le fait de tourner la roue droite dans le sens anti-horaire.

1 - Résoudre les billes noires et rouges :

Sur ma version, il y a 10 billes rouges, 10 noires, 9 jaunes et 9 bleues. On commence par remettre ensemble toutes les billes noires et toutes les billes rouges. Cela se fait intuitivement, nulle besoin d'indiquer une méthode.

2 - Finir :

Pour terminer la résolution, c'est-à-dire remettre les billes bleues ensemble et les jaunes ensemble, on va utiliser un petit commutateur qui a pour but de réaliser l'échange suivant :
 

Il suffit de faire [L5,R5] = L5 R5 L-5 R-5. Ce commutateur réalise deux transpositions indépendantes. L'idée est de commencer par faire un set-up qui ramène deux billes à échanger aux positions des billes jaunes et rouges échangées sur la photo ci-dessus.

Par exemple, supposons qu'on veuille réaliser l'échange suivant :
 

On commence par appliquer le set-up L-3 R7 :
 

 

Ce set-up a donc ramené les deux billes à échanger aux emplacements souhaités (Trait vert du haut). Elles vont être échangées par le commutateur. Ce dernier va aussi échanger deux autres billes qui sont toutes les deux noires, ce qui n'aura visuellement aucun effet. On obtient le résultat suivant :
 

 

Ensuite, on défait le set-up (R-7 L3) pour obtenir l'effet désiré :
 

On remarque que ce qui fait le succès de cette opération, c'est le fait que tandis qu'on échange deux billes bleues et jaunes, les deux autres échangées sont noires. Cette particularité impose une restriction sur le choix des billes à échanger. Il faut tourner la roue droite au moins de 5 billes dans le sens horaire afin d'avoir deux billes noires aux positions qui vont être échangées en bas.
 

Avant de commencer, je précise que la difficulté de ce casse-tête dépend du type de mélange. Si on se contente de mélanger l'Helicopter en n'utilisant que des demi-tours, on évite la plus grosse difficulté qui est de replacer les centres. Je m'explique. On constate vite en manipulant le casse-tête que les centres sont répartis sur 4 orbites, du moins tant qu'on se contente de demi-tours. Mais il est possible de faire passer un centre d'une orbite à une autre, en utilisant ce que j'ai tendance à appeler des mélanges "exotiques", c'est-à-dire des mélanges utilisant des cinquièmes de tour (Environ un cinquième. En fait, si on fait le calcul, on trouve 70,53° environ et non pas 72°. Mais bon, on continuera à dire un cinquième de tour).

Voici la position du casse-tête après une rotation d'un cinquième de tour :
 

La méthode que je présente ici commencera par s'occuper du cas des mélanges classiques, sans cinquième de tour.

1 - Notations :

On va utiliser des notations intuitives. On notera par exemple UF la rotation autour de l'axe passant par le centre du cube et le milieu de l'arête UF. Pour préciser l'angle, on notera (UF,1/2) pour dire qu'on effectue un demi-tour autour de l'axe UF. On utilisera les conventions mathématiques usuelles : une fraction positive désignera une rotation dans le sens trigonométrique (anti-horaire) et une fraction négative une rotation dans le sens contraire (horaire).
 

2 - Placement des centres (sans mélange "exotique") :

Tout se fait de façon très intuitive. Le mieux, il me semble, est de commencer par reconstituer une face puis la première moitié du cube contenant cette face. On termine ensuite par les centres de la deuxième moitié.

Il faut faire attention au schéma de couleurs du cube. En effet, comme aucun centre ne nous aide pour savoir où placer les couleurs, il est indispensable de s'aider des seules pièces donnant un renseignement à ce sujet : les coins.

3 - Placement des coins :

On va utiliser, pour cette étape, des cinquièmes de tour :
(UL,1/5) (RF,1/5) (UF,1/2) (RF,-1/5) (UL,-1/5) (UF,1/2) (LF,-1/5) (UR,-1/5) (UF,1/2) (UR,1/5) (LF,1/5) (UF,1/2)

Les photos suivantes montrent la première moitié de cet algorithme (qui servira à nouveau dans la partie concernant le placement des centres dans le cas de mélanges "exotiques") :

L'algorithme en entier échange les deux coins ULF et URF.

Remarque importante sur l'orientation des deux coins échangés : les deux coins réalisent un demi-tour par rapport à l'axe UF. Cela veut dire que si on échange deux coins adjacents en utilisant cet algorithme, ils auront nécessairement l'orientation qu'ils auraient si on se contentait de faire une simple rotation (UF,1/2).

Pour finir le cube, on procède donc à des échanges deux à deux de coins, en faisant attention à leur orientation. Pour pallier au problème de l'orientation, il est nécessaire d'avoir recours à des set-ups. Il ne faut pas hésiter à "promener" une pièce d'un emplacement à un autre afin qu'elle se trouve dans l'orientation requise avant de procéder à l'échange.

Si un coin est à sa place mais mal orienté (un autre aussi est alors mal orienté), on commence par échanger ce coin avec l'autre mal orienté. Ensuite, en faisant le set-up approprié, on place ces deux coins côte à côte en faisant attention à leur orientation puis on les échange à nouveau. On défait le set-up et c'est bon.

4 - Placement des centres dans le cas de mélanges "exotiques" :

On suppose qu'on a ramené le casse-tête sous forme de cube. On reprend la moitié de l'algorithme présenté dans la partie précédente :
(UL,1/5) (RF,1/5) (UF,1/2) (RF,-1/5) (UL,-1/5) (UF,1/2)

Observons l'effet obtenu :
 

On constate que deux paires de centres ont été transposées, ce qui a eu pour effet de changer d'orbite les deux pièces opposées (verte et bleue ici). Attention : il ne faut pas croire qu'il ne s'est rien passé pour les deux autres pièces transposées ! Elles n'ont peut-être pas changé d'orbite mais ne peuvent pas être rééchangées seules !

Toute l'astuce à présent est d'utiliser le changement d'orbite décrit ici à bon escient, avec, en adjonction, des set-ups adéquats.




 

Cette méthode nécessite d'être à l'aise sur les 3-cycles à la façon du Dino Cube (Rien de bien méchant, donc...).

1 - Former les paires d'arêtes à deux stickers :

On commence par former toutes les paires de deux arêtes ayant deux stickers. On s'en sort très bien intuitivement.

Une idée qui fonctionne bien est de former un maximum de paires au feeling puis, pour les dernières, on s'arrange à coup de set-up pour remonter trois arêtes à faire cycler sur un même étage. On peut pour cela utiliser un des deux étages marqués par une flèche sur la photo suivante :
 

Une fois les trois arêtes à faire cycler sur le même étage, on tourne l'étage et on défait le set-up. C'est facile !

Cependant, il faut faire attention à un petit problème qui peut survenir si on ne fait pas gaffe. L'étape d'après, il faudra remettre ces paires d'arêtes à leur place. Il se peut qu'une paire d'arêtes seulement ne soit pas orientée comme il faut, un peu comme le fameux problème de parité d'orientation qu'on rencontre sur un 4x4x4. Pas le choix, il faudra la retourner. C'est pourquoi il vaut mieux s'en rendre compte tout de suite.

Pour retourner la paire d'arête, on peut procéder en deux temps en faisant deux 3-cycles. Par contre, ce n'est pas la peine d'essayer de les échanger en une fois. C'est peut-être faisable mais je ne pense pas qu'il existe de formule simple pour ça.

Pour finir, il se peut aussi qu'on rencontre le deuxième problème de parité du 4x4x4 dû cette fois-ci au placement des arêtes. En clair, il peut arriver qu'on ait à échanger deux blocs de deux arêtes. Même principe que pour l'autre cas de parité : on procède en deux 3-cycles.

2 - Placer les blocs d'arêtes formés :

Pour cette étape, on fait comme s'il s'agissait d'un Jing's Pyraminx. Si on a évité les cas de parité expliqués dans la partie précédente, il n'y a pas de souci. On fera bien attention à placer correctement les centres de chaque face (les petits triangles en plein centre des faces).

3 - Résoudre toutes les arêtes :

C'est l'étape la plus simple. Elle se fait à grands coups de 3-cycles, comme sur un Pyraminx pour ce qui est des arêtes du milieu ou comme sur un Mosaic Cube par exemple pour ce qui est des arêtes extrêmes.

4 - Résoudre les centres :

Pour résoudre les petits triangles qui forment les centres, on va utiliser un commutateur. Posons quelques notations :
 

 
Pour exécuter le commutateur, on tiendra la face F devant soi, U étant au-dessus. r désigne la rotation du coin se trouvant en haut à droite (limité par les pointillés). M est une rotation de tranche. ATTENTION : petite erreur sur la deuxième photo : c'est le mouvement M' qui est dans le sens de la flèche et non pas M !

Le but du commutateur est ici de replacer les trois centres mal positionnés (bleu, vert et rouge).

On utilise [Fr'F',M] = Fr'F'MFrF'M'. Le pivot du commutateur est la tranche M. On remarquera en effet que les mouvements Fr'F' ne modifient qu'une seule pièce sur cette tranche (Ils ramènent la pièce rouge à la place de la bleue). Le mouvement M se contente donc de remplacer la pièce s'y trouvant (rouge à ce moment là du commutateur) par la pièce verte. FrF' ramène cette pièce verte à sa place et M' replace la tranche dans sa position initiale. On remarque donc qu'on pourrait très bien faire M' au lieu de M dans le commutateur. Ceci aurait juste pour effet de ne pas faire cycler les mêmes pièces.

Pour finir le casse-tête, il suffit donc d'utiliser ce commutateur en ayant au préalable effectué les set-ups adéquats.
 

Voici une page généraliste qui a pour but d'expliquer le principe des commutateurs et de montrer comment l'exploiter pour la résolution de nombreux casse-têtes.

1 - Qu'est-ce qu'un commutateur ?

La notion de commutateur est tout d'abord une notion mathématique de théorie des groupes. Dans un groupe, on appelle commutateur un élément noté [a,b]=aba'b' où a et b sont deux éléments du groupe et a' et b' leur inverse. a et b commutent si et seulement si [a,b] est l'élément neutre du groupe.

Cependant, ce n'est pas tant leurs propriétés mathématiques que leurs effets sur les casse-têtes qui nous intéressent. Avant d'aller plus loin, je tiens à remarquer que tous les commutateurs ne sont pas intéressants pour la résolution de puzzles de type Rubik's cube, ou du moins, pour être plus juste, tous n'ont pas le même intérêt.

En effet, prenons le commutateur [R,U] = RUR'U' sur un 3x3x3. Il réalise un cycle de trois arêtes (un 3-cycle, donc) et une double transposition de coins. Le défaut de cette formule est qu'elle déplace un peu trop de pièces. Son utilisation est donc difficile (quoique pas impossible) pour résoudre un 3x3x3.

On comprend dès lors qu'on préférera les commutateurs ne faisant bouger qu'un minimum de pièces. Pour des raisons mathématiques, il est souvent obligatoire de déplacer un minimum de trois pièces (comme sur un 3x3x3 où il est impossible de n'échanger que deux arêtes ou deux coins). On essayera donc au maximum de trouver des commutateurs réalisant un 3-cycle.

2 - Principe de construction d'un "bon" commutateur :

Un bon commutateur doit donc déplacer le minimum de pièces.

Pour réaliser cette opération, on procède ainsi :
- On réalise une suite de mouvements qu'on note A dont l'objectif est de remplacer une pièce (1) par une autre (2).
- On échange (2) avec une autre pièce (3) par une suite de mouvements qu'on note B.
- On exécute A' puis B' ce qui a pour but d'envoyer (1) à la place de (3), tout en remettant les autres pièces du casse-tête à leur place.

Au final, (1) est remplacé par (2), qui est remplacé par (3), qui est remplacé par (1). On a réalisé le cycle 1 -> 3 -> 2 -> 1. On le note (1 3 2) en mathématiques.

Pour que cette méthode fonctionne bien, il est nécessaire que les suites de mouvements A et B n'interfèrent pas trop entre elles (Je pourrais être plus précis mais je n'ai pas envie de compliquer un peu plus le propos).

Dans le meilleur des cas, on fera en sorte que A ne remplace qu'une seule et unique pièce (1) d'une face (appelée pivot dans la suite) par une pièce (2) située ailleurs, de façon à ce que B, par une simple rotation de cette face, remplace la pièce fraîchement arrivée (2) par une autre (3) de cette même face. A' renverra donc (3) à la place initiale de (2) et la remplace par (1). Enfin, B' envoie (1) à l'emplacement initial de (3) et ramène (2) à la place initiale de (1).

 

J'ai repris les notations de la partie précédente. 1, 2 et 3 sont les pièces à déplacer et les deux T les emplacements de transit. Les deux premières photos représentent la position de départ. On a trois pièces à faire cycler. 3 doit aller à la place de 2, 2 à la place de 1 et 1 à la place de 3. 

On note L et R les "faces" du Dino qui vont intervenir dans le commutateur intéressant.

On utilise le commutateur [R',L] = R'LRL'. Dans cet exemple, on a donc A = R' et B = L. La face L, entourée de lignes vertes, est celle qui constitue le pivot du commutateur : c'est sur cette face que se situent les deux pièces 1 et 3. Et c'est sur cette face que le mouvement A remplace une pièce sans rien modifier d'autre. Ainsi, on peut faire tourner la face (mouvement B), de sorte à remplacer la pièce nouvellement arrivée par une autre de la même face. En refaisant A puis B à l'envers, on remet le cube dans son état initial.

Les quatre photos qui suivent montrent le résultat de chaque étape du commutateur. On retrouve exactement le déroulement indiqué dans la partie 2.
 

 

Ici, A = R'D'R et B = U'. Le commutateur est [A,B] = R'D'RU'R'DRU. Les images 2 à 5 donnent le résultat de chaque étape A, B, A' et B'. Le pivot est la face U.

Cet exemple permet, je trouve, de bien comprendre ce que doit être un bon commutateur. Le mouvement A a pour effet de remplacer le coin 1 par le coin 2. Mais remarquons bien que pour la face U, c'est la seule pièce modifiée par A. Ainsi, B ne fait que remplacer le coin modifié par le coin 3. A' reconstitue le cube sans rien altérer, ce qui est normal puisqu'à part la face U qui a tourné, rien ne s'est produit entre la fin de A et le début de A' : le reste du cube n'a pas été modifié et A' remet forcément à leur place toutes les pièces qui ont été déplacées par A. On retrouvera exactement la même logique sur la Dayan Gem III.

Bien des algorithmes sont inspirés de ce principe. Le classique Niklas du 3x3x3 (RU'L'UR'U'LU = [R,U'L'U] Le pivot est la face B) est une variante de ce principe.

 
Précisons un peu les notations. U est la face du dessus, F la face de devant supérieure et f la face de devant inférieure. 1, 2 et 3 sont trois coins de la Dayan Gem III.

Ici, A = F'fF et B = U. Le commutateur est [A,B] = F'fFUF'f'FU'. Les images 2 à 5 donnent le résultat de chaque étape A, B, A' et B'. Le pivot est la face U.

On exploite sur cet exemple le même principe que dans l'exemple précédent : le mouvement A ne modifie qu'un seul coin de la face U, ce qui permet de tourner cette dernière librement afin de remplacer le coin modifié par le coin 3. Je ne détaille pas la suite, j'espère que vous commencez à comprendre !

J'ai pris comme un exemple un 5x5x5. On veut ici, en apparence, échanger les deux centres mal placés. Je dis bien en apparence car, comme très souvent, il n'est pas possible d'effectuer une simple transposition. On va donc réaliser un 3-cycle et pour cela utiliser un commutateur.
 

Ici, A = dr'd'r (qui, remarquez, est déjà un commutateur !) et B = U. Le commutateur est [A,B] = dr'd'rUr'drd'U'. Le pivot est la face U.

La cinquième image montre l'état du cube après A. Le résultat de cette étape est que 2 se trouve alors à la place de 1.

L'image d'après, B = U envoie 3 à la place de 2. A' redescend 3 à la place initiale de 1 et B' replace 1 et 2 là où ils doivent être.

Une fois qu'on a compris ce qui se passe dans cet exemple, on peut généraliser ce procédé à n'importe quel cube et n'importe quel emplacement.

f) Les centres du Face Turning Ocathedron :
 

On utilise ici A = R'LR et B = M'. Le commutateur est [A,B] = R'LRM'R'L'RM. Le pivot du commutateur est la tranche M. Encore une fois, le mouvement A ne modifie qu'une seule pièce sur le pivot : seul le centre 1 est remplacé par un autre (2) sur la tranche M. On peut alors exécuter le mouvement B (M' mais on pourrait aussi faire M) qui n'a pas d'incidence sur le reste du casse-tête.

C'est toujours le même principe !

Le principe est relativement simple. Imaginons que nous sachions faire cycler trois pièces d'un casse-tête à l'aide d'un commutateur noté B à la condition qu'elles se trouvent exactement à trois positions données 1, 2 et 3. Imaginons que nous devions faire cycler trois pièces non forcément situées aux emplacements 1, 2 et 3. On commence alors par réaliser une série de mouvements notée A qui ramène chacune des pièces à faire cycler sur les emplacements 1, 2 et 3. On exécute alors B qui fait cycler les trois pièces qui nous intéressent. B ne déplaçant rien d'autre que ces trois pièces, on peut ensuite exécuter A' pour tout remettre en ordre et renvoyer les pièces à présent déplacées aux trois emplacements qu'elles occupaient avant la manipulation.

Voici une méthode plutôt facile à mettre en oeuvre. C'est une méthode de réduction. On se ramène petit à petit à la résolution d'un casse-tête du type Dino Cube.

Il est nécessaire de savoir résoudre un Dino Cube (donc d'avoir une idée de comment réaliser un 3-cycle sur ce type de casse-tête), de savoir former les paires d'un 4x4x4 et de savoir faire un set-up, quel que soit le casse-tête.

Pour placer les centres comme il faut, il faut déjà connaître le schéma de couleurs. Si on ne l'a pas noté avant, on peut le retrouver en observant attentivement les coins puisque les stickers en forme de losange sont de la couleur des centres. A partir de là, il est impératif de faire attention à ne plus modifier le placement des centres, sans quoi on se retrouverait dans un cas impossible à résoudre.

2 - Placer les triangles qui sont seuls :

Il s'agit des triangles qui ne vont pas par paire, c'est-à-dire ceux qui se trouvent seuls entre deux coins. Cette étape est plutôt intuitive. On réalise des 3-cycles en utilisant des mouvements du type ABA'B'.

3 - Formation des paires de coins :

On reforme toutes les paires de coins qui entourent un groupe de deux petits triangles opposés par le sommet. On ne cherche pas à placer ces paires à leur place. On se contente de les reformer.

Pour y parvenir, on utilise des commutateurs qui ressemblent à ceux qu'on peut utiliser dans la formation des paires d'arêtes sur un 4x4x4. En gros, on reforme une paire en utilisant une suite de mouvements A, on remplace ensuite la paire formée par une autre puis on exécute A'. En faisant attention, on réussit sans difficulté à reformer toutes les paires.

4 - Placement des petits triangles :

C'est l'étape qui m'a demandé un peu de recherche !

Tout d'abord, introduisons quelques notations. Notons 1 et 2 les rotations suivantes :
 

Précisons. Pour le mouvement 1, c'est la partie droite du casse-tête qui tourne dans le sens horaire. Pour le mouvement 2, c'est la partie gauche qui tourne dans le sens anti-horaire.

La face grise de la photo (qui apparaît un peu blanche...) est la face U.

Ensuite, on numérote certains triangles :
 

La photo de gauche montre le casse-tête légèrement tourné vers la gauche. Le numéro 2 désigne le triangle qu'on ne voit pas sur la photo mais qui se trouve juste en face de celui où pointe la flèche. Celle de droite le montre un peu relevé de façon à voir la face du dessous.

Bon, la formule à présent. Le commutateur 1 2' 1' 2 U' 2' 1 2 1' U réalise le cycle des triangles (1,2,3,4,5). A grand coup de set-up, on reconstitue tous les blocs deux coins + deux triangles. Le principe du set-up est d'amener aux emplacements de 1 à 5 les pièces qu'on a envie de faire cycler en utilisant une série de mouvements qu'on refait à l'envers après le cycle.

5 - Fin

La fin est à présent très simple et se fait de façon intuitive en 3-cycles à la façon du Dino Cube.

Après m'être bien cassé la tête sur ce puzzle, je vais essayer de décrire la solution que j'ai trouvée.

Elle se déroule en quatre étapes :

1) Placement des arêtes
2) Placement des coins, sans se soucier de leur orientation
3) Orientation des coins
4) Placement des centres

Avertissement : cette solution présuppose de savoir résoudre un Rainbow Cube.

Entrons dans le détail :

1) Placement des arêtes :

Il s'agit ici de ne considérer que les arêtes. Elles sont au nombre de 12.

Si on néglige totalement le reste du puzzle, on s'aperçoit que le placement des arêtes se ramène à la résolution d'un Rainbow Cube. Cette résolution ne devrait pas poser de problème, surtout qu'elle est très intuitive.

Je conseillerais tout de même de commencer par une face puis de compléter petit à petit les autres en finissant par la face opposée à la première.

2) Placement des coins :

Tout d'abord, une petite photo pour fixer quelques notations :
 

On appelle donc U et R deux faces ayant une arête en commun.

La séquence suivante permet d'effectuer le cycle des sommets (123) : (R'URU)x2

En l'effectuant quelques fois, on arrive à placer tous les coins à leur place.

3) Orientation des coins :
 
Changement de notations pour cette étape :
 

U et R ne se touchent que par un sommet. D est la face opposée à U.

La séquence suivante permet l'orientation des deux coins marqués en jaune :
(R'DRD'R'DR)U'(R'D'RDR'D'R)U

A répéter au maximum trois fois.

4) Placement des centres :
 
Quelques notations :
 

Pour réaliser le cycle des centres (1 3 2), on utilise le commutateur [R'LR,M'] = R'LRM'R'L'RM. Le pivot du commutateur est la tranche M. R'LR déplace 2 à la position 1 et c'est la seule pièce de la tranche M qui est modifiée. A ce stade, on pourrait aussi faire M au lieu de M'. Ce serait une juste autre pièce que 3 qui entrerait dans le cycle.

Le plus souvent, les méthodes qu'on trouve sur internet, dont certaines très efficaces, présentent un même défaut : il est nécessaire d'apprendre un nombre parfois élevé de formules qui sont le plus souvent assez obscures. J'entends par là qu'il est souvent bien difficile de comprendre pourquoi la formule a l'effet désiré, ce qui peut parfois bien compliquer la mémorisation.

Le but de cette méthode est de montrer, moyennant tout de même un peu d'entraînement, qu'on peut résoudre le Rubik's Cube sans répéter des formules apprises "bêtement". Elle développe des idées basées sur l'intuition et l'observation. Il suffit de comprendre (et non d'apprendre !) quelles sont les clés de ces idées pour résoudre le cube. Evidemment, l'intuition et les qualités d'observation ne sont pas des choses innées chez la plupart d'entre nous et forcément, il faudra travailler pour aiguiser ses sens.

Volontairement, j'évite donc tous les algorithmes "classiques" de type belge ou chaise. Pour les initiés, je dirais juste que la méthode est basée exclusivement sur l'emploi de cycles et de commutateurs qui une fois bien compris permettent vraiment une résolution intuitive.

Autre détail : inutile d'essayer de faire du speedcubing avec cette méthode, ce n'est pas du tout son but !

Enfin, étant donné que c'est la première fois que je me lance dans un tutoriel complet sur le Rubik's Cube, il se peut que je ne sois pas suffisamment clair. Pour toute remarque ou question, n'hésitez pas à me contacter (Onglet "Me contacter") ou à commenter directement cet article.

Bon, c'est parti.




On suppose connues les notations internationales habituelles. Si vous ne les connaissez pas, vous pouvez les apprendre ici.

La méthode se déroule en deux grandes étapes :

Ce n'est pas une méthode couronne par couronne (layer by layer) comme on recommande souvent d'apprendre aux débutants. Elle s'appuie sur le fait que résoudre les arêtes est facile tant qu'on ne s'embarrasse pas des coins. Résoudre ensuite les coins sans toucher aux arêtes n'est pas un problème, comme on le verra.

Remarques : Cet article est la deuxième version de mon tutoriel. Je l'espère plus clair et mieux structuré que mon premier essai. Pour le rendre plus lisible, je l'ai agrémenté d'applets java dues à Werner Randelshofer. Vérifiez que votre pluggin java est à jour ! Ces applets sont faciles d'utilisation et permettent, à l'aide de la souris, de tourner le cube dans tous les sens et de visualiser étape par étape les manipulations à effectuer sur le cube.

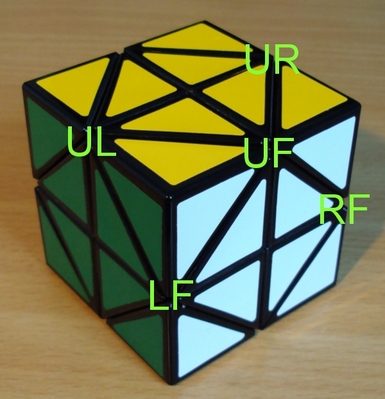
Le but de cette première étape est d'arriver à cette configuration, ou à toute autre configuration similaire (N'hésitez pas à tourner le cube dans tous les sens avec la souris !) :


Pour commencer, on réalise une croix sur une face, étape qui ne pose en principe aucun problème à qui a déjà manipulé un peu un Rubik's cube :



Ensuite, on met à leur place trois des arêtes constituant la deuxième couronne. Pour y parvenir, on peut utiliser une des deux passes suivantes :


Cette manipulation est très simple et doit devenir complètement instinctive. On place donc trois arêtes convenablement. Si une arête est à sa place mais mal orientée, il faut la déplacer. On n'oublie pas que le but de la première étape est de placer et d'orienter toutes les arêtes, donc il ne faut pas laisser d'arête mal orientée.

Si à ce stade les arêtes du cube sont toutes à leur place, ce qui arrive rarement mais n'est pas impossible, on passera à l'étape c. Orientation des arêtes.

Si ce n'est pas le cas, on laisse un emplacement vide sur la deuxième couronne car celui-ci va servir à faciliter la résolution des arêtes de la dernière face. Si le hasard fait que les quatre arêtes de la deuxième couronne sont correctement placées, il est nécessaire pour la suite de sortir tout de même une des quatre arêtes.

b. Finir le placement des arêtes :

Dans toute la suite de cette première étape, on va exploiter un unique grand principe :
 

Si X et Y sont deux faces adjacentes du cube, toute manipulation du type XYX'Y', X'YXY', XY'X'Y' ou X'Y'XY réalise un cycle de trois arêtes.

Dans ce grand principe, X et Y peuvent aussi désigner des demi-tours sur deux faces adjacentes. En étant astucieux et observateur, on peut alors s'en sortir pour finir le placement et l'orientation des arêtes. Tout ce qui suit n'est finalement là que pour l'exemple.

On commence par faire tourner la dernière face (opposée à la première croix réalisée) jusqu'à ce qu'un maximum d'arêtes soient à leur place. Attention : à leur place ne veut pas dire forcément bien orientées ! On s'occupera des éventuels problèmes d'orientation après.

Trois cas peuvent alors se produire : il peut y avoir une, deux ou trois arêtes bien placées. Mais il va falloir dans tous les cas se ramener au cas où seules deux arêtes de la dernière face sont à leur place.

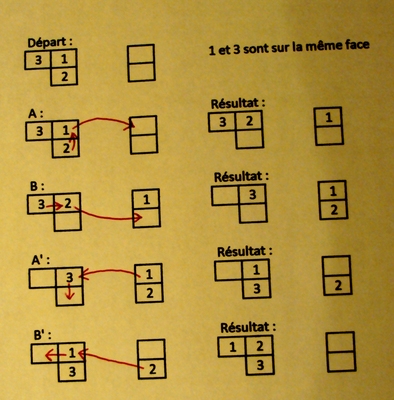
Dans le cas où une seule arête est à sa place, on peut par exemple procéder ainsi :


Remarquez bien la position de l'arête initialement bien placée (bleue orange). Notez aussi que, conformément au grand principe annoncé, seules trois arêtes ont réalisé un cycle (Bleue-Jaune, Rouge-jaune et Bleue-rouge).Si vous n'êtes pas dans ce cas, essayez un autre cycle ou déplacez l'arête bien placée à cet endroit en faisant tourner la face U autant que nécessaire. Dans tous les cas, il est nécessaire de ne pas mettre à sa place la dernière arête de la deuxième couronne.

Pour le cas où trois arêtes sont à leur place, on procède de façon similaire :


Ici, les trois arêtes qui ont cyclé sont les arêtes Bleue-Orange, Bleue-Rouge et Bleue-Jaune.

Enfin, une fois qu'on se trouve dans le cas où deux arêtes sont connectées, on fait cycler les trois arêtes qu'il reste à placer. Il y a deux cas : soit les deux arêtes restantes sur la face supérieure sont adjacentes, soit elles se font face :


c. Orientation des arêtes :

Une fois placées toutes les arêtes, il se peut que certaines soient mal orientées. Quitte à tourner le cube, on les place sur la face U.

Commençons par le cas où les deux arêtes à orienter sont adjacentes. L'idée est de faire d'abord cycler trois arêtes dont les deux mal orientées (en faisant FR'F'R) puis de refaire cycler dans l'autre sens ces mêmes arêtes (U'RUR') en tenant compte cette fois-ci de l'orientation :


 
Pour le cas où deux arêtes l'une en face de l'autre sont mal orientées, on pourra par exemple se ramener au cas précedent en utilisant la même méthode pour orienter une des deux arêtes mal orientées et une des deux arêtes bien orientées de la même face.

Si deux arêtes à orienter ne se trouvent pas sur la même face, il suffira de faire ce que dans le jargon du cube on appelle un set-up. L'idée qui n'a rien de bien méchant est de ramener côte à côte sur la même face les deux arêtes à orienter. En principe, ce doit être possible en deux rotations maximum qu'il faut mémoriser : c'est le set-up. On effectue alors le changement d'orientation en utilisant encore une fois la démarche expliquée ci-dessus puis on refait à l'envers le set-up.

Conclusion de la première étape :

Dans toute cette étape, tout est intuitif, une fois qu'on a compris le principe de base encadré plus haut. Il est recommandé, pour bien maîtriser cette méthode, de s'entraîner à réaliser des cycles de trois arêtes. En effet, si on comprend bien ce qui se passe quand on réalise les cycles, on peut même éviter d'avoir à retourner d'éventuelles arêtes mal orientées.

2. Placement et orientation des coins :

a. Placement des coins :

Si les coins sont tous placés, on passe à l'étape b. Orientation des coins.

Comme annoncé dans l'introduction, cette étape est très simple. Elle est basée aussi sur un cycle de trois pièces du cube, ici trois coins. L'idée est de choisir trois cubes à cycler dont deux situés sur la face U, et le troisième sur la face D. Pour se ramener à cette configuration, on peut être amené à tourner une face du cube d'un quart ou d'un demi tour (principe du set-up à nouveau). Il suffira juste de refaire cette manipulation à l'envers après le cycle.

Le principe essentiel est le suivant : si on est capable de trouver un algorithme X qui remonte un coin C1 de la face D sur la face U sans rien changer d'autre sur la face U, alors on peut réaliser les cycles de trois arêtes souhaités. Il suffira, après X, de tourner la face U de façon à échanger le coin modifié avec un autre coin C2 puis d'appliquer X'. Ainsi, le coin C2 redescendra en D à la place de C1. C1 se trouvera face U à la place d'un troisième coin C3 qui lui aura pris la place du coin C2.

Pour X, on peut prendre par exemple l'algorithme R'DxR où x désigne un nombre de 1 à 3. Il ne modifie en effet qu'un seul coin de la face U.

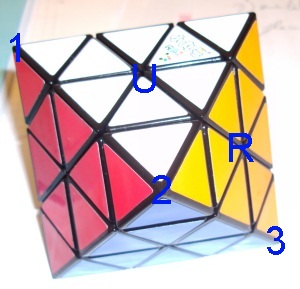
Petit exemple :

Cet algorithme fait cycler les coins Rouge-Bleu-Blanc, Rouge-Bleu-Jaune et Rouge-Vert-Jaune. La séquence R' D' R fait remonter le coin Rouge-Bleu-Jaune à sa place, chassant le coin Rouge-Bleu-Blanc. U' remplace le coin Rouge-Bleu-Jaune fraîchement arrivé sur la face supérieure par le coin Rouge-Vert-Jaune. R' D R redescend ce dernier et remonte à sa place le coin Rouge-Bleu-Blanc qui avait été mis à l'écart. U replace le cube dans son état initial.

Remarquons que dans cet exemple, le coin est arrivé bien orienté. Il a donc réalisé une rotation d'un quart de tour dans le sens inverse des aiguilles d'une montre autour de l'axe rouge. Mais évidemment, l'orientation initiale du coin influence l'orientation du coin après le quart de tour. Il est par conséquent essentiel de se familiariser avec le symétrique de cette situation. On peut par exemple prendre pour X l'algorithme LDL', ce qui permettra un quart de tour dans le sens des aiguilles d'une montre.

Conclusion de l'étape 2.a :

Il suffit d'apprendre à jouer avec ce principe et le placement des coins deviendra un jeu d'enfant. En étant attentif, on peut même éviter une grosse partie des problèmes d'orientation des coins, thème de la dernière partie de cette méthode.

b. Orientation des coins :

L'idée générale de cette étape a un point commun avec celle de la précédente : on va utiliser un algorithme X qui oriente correctement un coin de la face supérieure sans rien changer d'autre sur cette face.

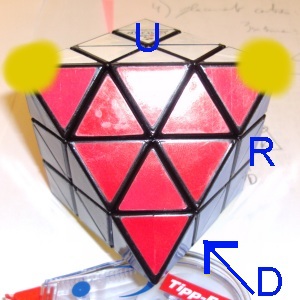
Petit exemple. On part de cette configuration :
 
L'algorithme qu'on va présenter tout de suite va réorienter les deux coins Bleu-Rouge-Jaune et Bleu-Rouge-Blanc à la fois. L'idée est d'utiliser X=R'DRD'R'DR, qui oriente le coin Bleu-Rouge-Jaune en le faisant tourner d'un tiers de tour dans le sens des aiguilles d'une montre, puis de remplacer ce coin par le coin Bleu-Rouge-Blanc en faisant U'. En appliquant X à l'envers, on applique alors à ce dernier une rotation d'un tiers de tour dans le sens inverse des aiguilles d'une montre et donc on l'oriente comme désiré. Un U final est nécessaire pour compenser le U' précédent.

En résumé, on a donc :
Si par hasard deux coins opposés de la même face sont mal orientés, on procède de même en échangeant à mi-parcours les deux coins en faisant U2 au lieu de U.

Enfin, si deux coins à orienter ne sont pas sur une même face, on y remédie par un petit set-up d'un demi-tour d'une des faces portant un des coins à orienter qui permet de se retrouver dans la configuration précédente, avec les deux coins à orienter côte à côte sur la même face. On finira alors par faire à l'envers ce demi-tour.

Conclusion de cette dernière étape :

Dans cette étape, il ne s'agit pas d'apprendre par coeur l'algorithme X mais vraiment de comprendre comment il oriente le coin en FRU. En l'utilisant plusieurs fois, on finit ainsi la résolution du cube.